J’ai réalisé un régulateur PID pour la gestion d’une vanne thermostatique Z-Wave Spirit en mode manuelle (fonctionnement en %). Parce que moi je veux que ça commence avec du pied au plancher (vanne ouverte à 100%) à 5h le matin pour que ça monte rapidement en température ![]()
Le régulateur calcule une valeur d’ouverture de vanne comprise entre 0% et 100% à envoyer à la tête thermostatique en fonction de l’écart entre la température mesurée et la température de consigne afin de réguler la température de la pièce à partir d’une sonde de température de votre choix.
Un peu de lecture
Pour comprendre plus facilement la régulation PID avec les mains, je vous conseille de lire la première partie de cette page Implémenter un PID sans faire de calculs ! » Sciences et Techniques
Je vous invite également à lire cette page Principes de régulation : P - PI - PID - Energie Plus Le Site qui explique super bien les types de régulation P et PI pour le chauffage.
Enfin, pour l’explication plus théorique de ce type de régulateur, je vous laisse lire la page Wikipedia Régulateur PID — Wikipédia
Fonctionnement
Le régulateur PID calcule l’ouverture d’une vanne physique d’un radiateur entre 0% et 99% afin que la température mesurée dans la pièce atteigne la température de consigne. Il régule les têtes thermostatiques Spirit qui peuvent fonctionner en mode manuel où c’est à l’utilisateur de choisir l’ouverture de vanne en % (il n’y a plus de régulation interne au niveau de la tête thermostatique).
Pas de plugin
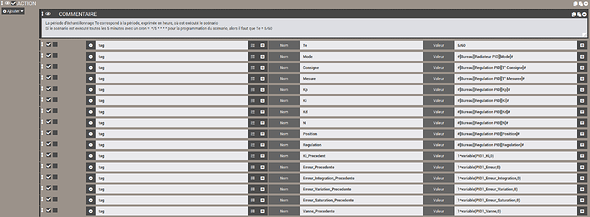
Comme je ne sais pas faire de plugin, j’ai créé un virtuel et un scénario qui tourne derrière avec quelques variables.
Virtuel
Le virtuel ne sert qu’à la visualisation et aux réglages du régulateur PID
Tout d’abord, il faut définir les températures de consigne et mesures
Réglages des coefficients
Choix du type de régulation parmi toutes les combinaisons P/I/D.
Pour le chauffage, ce sont les régulations P, PI et PID qui nous intéressent, à la rigueur une régulation I s’il n’y pas pas de changement de consigne ou pour bien comprendre le fonctionnement.
La position C permet de fixer un pourcentage d’ouverture de vanne lorsque l’erreur nulle, c’est-à-dire lorsque la température mesurée égale la température de consigne. Ce paramètre n’est utilisé que s’il n’y pas de correction Intégrale I. Si cette position C est nulle, la vanne est fermée lorsque la pièce est à température et le radiateur ne chauffe plus. Donc, il faut une erreur pour que la vanne s’ouvre et que la pièce chauffe (ceci est très bien expliqué dans le lien précédent). Pour commencer, il est préférable choisir une position médiane entre 25% et 50%.
Le coefficient Kp représente le gain proportionnel en % d’ouverture par degré d’erreur %/°C. Avec un Kp=30%/°C, un changement de +2°C sur la consigne fera augmenter l’ouverture de vanne de +60%.
Avec une régulation Proportionnelle, il y aura toujours une erreur résiduelle, c’est-à-dire toujours un écart avec la température de consigne.
Le coefficient Ki représente le gain de l’action intégrale en % d’ouverture par degré d’erreur cumulée %/(°C.h). L’action intégration permet de supprimer l’erreur résiduelle, l’écart final de température entre la mesure et la consigne. Donc l’action intégrale est nécessaire pour d’obtenir la température de consigne. Lorsque la température de consigne est atteinte, il n’y a plus d’erreur, le terme proportionnel est nul et il reste seulement le terme intégral. Exemple, avec un Ki=5%/°C.h, la vanne sera ouverte à 20% pour une erreur cumulée de 4°C.h après une montée en température.
Ki=Kp/Ti avec Ti qui correspond à la période d’intégration en minutes.
Le coefficient Kd représente le gain de l’action dérivée en % d’ouverture par variation d’erreur %/(°C/h). L’action dérivée permet au régulateur de réagir aux perturbations et de donner un coup de boost lors du changement de consigne. Exemple, lors d’un changement de +2°C sur la consigne, la variation d’erreur passe à 24°C/h pour un pas de calcul de 5 minutes. Plus le pas de calcul est petit, plus la variation d’erreur est grande. Celle-ci est ensuite multipliée par le coefficient Kd, ainsi le terme dérivé Kd * Erreur_Variation peut être très violent et l’ouverture/fermeture de vanne aussi. Je déconseille l’utilisation de l’action dérivée dans un premier temps.
Kd=Kp*Td avec Td qui correspond à la période de dérivation en minutes. Pour commencer, il est préférable de choisir Td=Ti/4
La dérivée de l’erreur est très sensible aux changements de consigne ainsi qu’au bruit de mesures (oui, une résolution de 0.1 °C même 0.625°C pour la température mesurée, c’est très bruité). C’est pourquoi, il est nécessaire de filtrer cette dérivée.
L’impact du filtrage est fixé par le coefficient N. N=0 signifie pas de filtrage du tout (la formule de filtrage n’est pas utilisée) mais inutilisable en pratique. Ensuite, plus N est grand, plus le filtrage est faible. Dans la littérature, il est souvent écrit de prendre N entre 5 et 20. Je trouve qu’avec N>3 le filtrage n’est pas suffisant. N=2 me parait satisfaisant.
On voit bien les changements de consigne sur la variation de l’erreur filtrée.
Affichage des coefficients précédemment choisis
Le régulateur (scénario) calcule les différentes erreurs dans des variables, le virtuel ne fait qu’afficher simplement ces variables.
- Erreur (Proportionnelle) : erreur entre la température de consigne et la température mesurée
- Erreur Intégration : erreur cumulée en degré heure (°C.h) de l’erreur proportionnelle
- Erreur Variation : variation d’erreur en degré par heure (°C/h)
L’ouverture de vanne est la somme des 3 actions Proportionnel P, Intégrale I, Dérivée D et d’un terme constant C lorsqu’il n’y a pas d’action Intégrale. Ceci permet d’un coup d’œil de savoir quelle action active principalement la vanne.
Les unités et les limites de réglages sont adaptés pour le chauffage. Mais le principe de régulation reste le même pour une autre utilisation.
Scénario
Passons à la partie la plus intéressante, le précieux code.
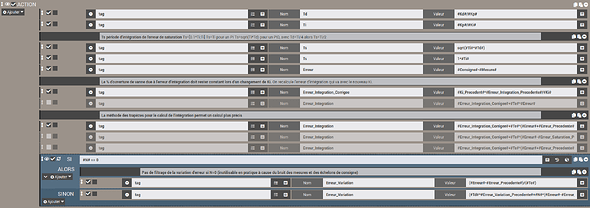
Toutes X minutes, le scénario récupère d’abord tous les paramètres dont il a besoin dans des tags.
Le scénario calcule les différentes erreurs quelque soit le type de régulation choisie. Cela permet de voir via le virtuel comment aurait pu se comporter le régulateur si telle correction avait été sélectionnée. Exemple, si je ne sélectionne pas la Dérivation, je visualise tout de même la variation d’erreur filtrée et j’ai juste à la multiplier par le coefficient Kd pour avoir une idée qu’aurait apportée la correction Dérivée.
Pour les formules qu’on ne voit pas entièrement
Erreur_Integration = #Erreur_Integration_Corrigee#+#Te#*(#Erreur#+#Erreur_Precedente#)/2
Erreur_Variation = (#Td#*#Erreur_Variation_Precedente#+#N#*(#Erreur#-#Erreur_Precedente#))/(#Td#+#N#*#Te#)
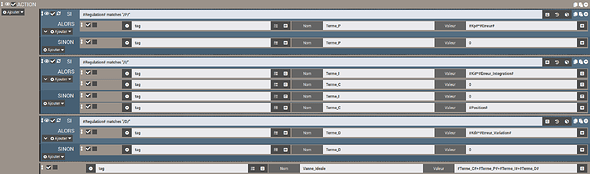
L’ouverture de vanne correspond à la somme des 3 corrections P I D plus la constante C s’il n’y a pas de correction I
La vanne physique ne peut pas prendre n’importe quelles valeurs, donc il faut limiter la vanne pour qu’elle reste dans l’intervalle 0% à 99%
Lorsque la vanne réelle arrive en butée 0% ou 99%, il ne faut plus continuer l’intégration de l’erreur. En effet, si par exemple la vanne se ferme suite à une baisse de consigne de plusieurs degrés (passage en mode Eco), la température réelle peut rester très longtemps (plusieurs heures) au dessus de la consigne. Pendant ce temps, l’erreur cumulée ne ferait que diminuer la vanne idéale dans des valeurs très négatives car pour le régulateur, il fait toujours trop chaud, donc il veut fermer davantage la vanne à chaque cycle. Lors d’une augmentation de consigne de plusieurs degrés (passage en mode Confort), il faudrait un certain temps (très long) afin l’erreur cumulée augmente pour faire revenir la vanne idéale vers des valeurs positives et pendant tout ce temps perdu, la vanne réelle resterait à 0%. L’idée est de venir retrancher l’erreur, que j’ai appelée erreur de saturation, en trop avant l’intégration pour que celle ci ne diverge pas.
Pour la formule complète
Erreur_Integration = #Erreur_Integration#-(#Ti#/#Ts#)*#Te#*(#Erreur_Saturation#+#Erreur_Saturation_Precedente#)/2
En fin de scénario, toutes les variables sont sauvées pour le prochain cycle
J’ai dû arrondir les valeurs afin d’éviter ce problème
C’est un peu moche comme code, mais en attendant que quelqu’un me propose mieux…
Bon, finalement l’astuce est est mettre des ' ' sur les tag des nombres qui peuvent être avec exposant pour que le calcul soit effectué correctement. Remarque, " " fonctionne aussi mais peut poser parfois des soucis sur certaines expressions en cas de double "" "".
Pour terminer, le scénario applique l’ouverture de la vanne si le radiateur est en mode régulation externe
Code source
Vous pouvez télécharger le code corrigé du scénario ici scenario_tag_quote.txt (7,5 Ko)
Afin de pouvoir importer facilement le scénario, il faut utiliser ce template corrigé PID_tag_quote.json.txt (74,3 Ko) (extension .txt est à enlever car c’est un fichier JSON)
J’en ai profité pour remplacer la syntaxe #MonTag# par tag(MonTag).
Conclusion
J’ai un peu galéré pour l’implémentation de certaines parties (le filtrage et la limitation de l’intégrateur) car la littérature ne parle que de choses théoriques. Je ne suis pas un expert en régulation, mes cours datent un peu et je ne travaille pas du tout dans ce domaine. Si vous voyez des erreurs dans l’implémentation ou que je raconte des conneries ou si avez des idées d’amélioration, n’hésitez pas.
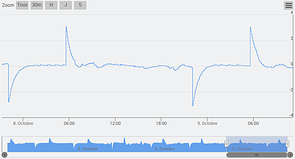
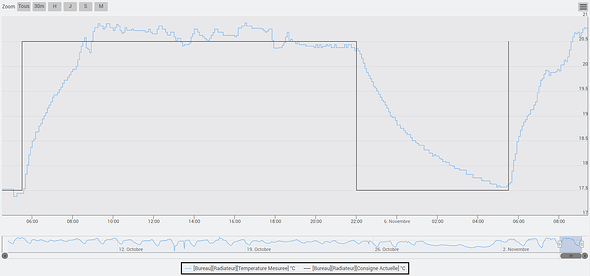
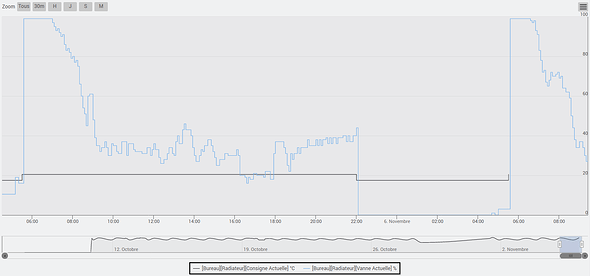
Résultats en images dans un petit bureau de 8m² avec une personne présente en journée 8h-18h.
Température mesurée en bleu et consigne en noir : 20.5° le jour et 17.5°C la nuit.
Remarque, comme il a fait assez froid dehors, j’ai perdu les 3°C dans la nuit entre 22h et 5h30 du matin.
Ouverture de vanne en sortie du régulateur.
La vanne commence la journée à 5H30 avec 100% d’ouverture les premières heures puis se termine vers 30%.